Ap calc bc unit 9 review – Embark on a journey through AP Calc BC Unit 9, where you’ll delve into the fascinating world of applications. From exploring the intricate relationship between curves to unraveling the mysteries of differential equations, this unit promises an adventure filled with insights and practical knowledge.

Prepare to uncover the secrets of finding areas between curves, calculating volumes of solids of revolution, and delving into the realm of differential equations to model real-world scenarios. Along the way, you’ll encounter parametric equations and polar coordinates, unlocking new perspectives on geometric shapes.

Dive deeper into the convergence and divergence of sequences, unravel the mysteries of series, and discover the power of vectors and matrices in solving systems of equations.

Integral Applications

Integrals have numerous applications in real-world scenarios, particularly in calculating areas, volumes, and work done by variable forces.

By utilizing the definite integral, we can determine the area between two curves. This technique involves subtracting the area below the lower curve from the area above the upper curve within the specified limits.

Volumes of Solids of Revolution

Integrals are also instrumental in calculating the volumes of solids of revolution. By rotating a region about a given axis, we can employ the method of cylindrical shells or disks to determine the volume of the resulting solid.

• Cylindrical Shells:Involves integrating the circumference of a cylindrical shell multiplied by its height.
• Disks:Involves integrating the area of a disk multiplied by its thickness.

Work Done by a Variable Force

Integrals play a crucial role in calculating the work done by a variable force. When a force varies with respect to distance, the work done can be determined by integrating the force function over the distance traveled.

Work = ∫ F(x) dx

Differential Equations: Ap Calc Bc Unit 9 Review

Differential equations are mathematical equations that involve the derivatives of unknown functions. They are used to model a wide variety of real-world phenomena, such as the motion of objects, the flow of fluids, and the growth of populations.

Separable Differential Equations

Separable differential equations are a type of differential equation that can be solved by separating the variables and integrating both sides of the equation. To solve a separable differential equation, follow these steps:

1. Rewrite the equation in the form

“`dy/dx = f(x)g(y)“`

2. Separate the variables by multiplying both sides by dx and dividing both sides by g(y)

“`(1/g(y))dy = f(x)dx“`

3. Integrate both sides of the equation

Cramming for the AP Calc BC Unit 9 review? Take a break and check out the AP Physics 1 Unit 2 FRQ for a quick brain teaser. Don’t worry, you’ll be back to conquering those integrals and derivatives in no time!

“`∫(1/g(y))dy = ∫f(x)dx“`

Solve for y.

Exact Differential Equations

Exact differential equations are a type of differential equation that can be solved by finding an integrating factor. An integrating factor is a function that makes the differential equation exact, meaning that it can be written in the form:“`M(x,y)dx + N(x,y)dy = 0“`To find an integrating factor for an exact differential equation, follow these steps:

Compute the partial derivatives of M and N with respect to x and y, respectively:

“`∂M/∂x = ∂N/∂y“`

• If the above equation is true, then the differential equation is exact.
• If the equation is not true, then find a function μ(x,y) such that:

“`μ(x,y)M(x,y) = ∂μ/∂y“`

4. The integrating factor is then given by

“`μ(x,y) = e^(∫(∂μ/∂x)/μ dx)“`

• Multiply both sides of the differential equation by the integrating factor μ(x,y).
• Solve the resulting equation for y.

Examples of Differential Equations in Real-World Scenarios

Differential equations are used in a wide variety of real-world applications, including:* Modeling the motion of a projectile

• Describing the flow of water in a pipe
• Predicting the growth of a population
• Analyzing the spread of a disease

Parametric Equations and Polar Coordinates

Parametric equations provide an alternative way to represent curves in the plane. They use two functions, \(x = f(t)\) and \(y = g(t)\), to describe the coordinates of a point on the curve as a function of a parameter \(t\).

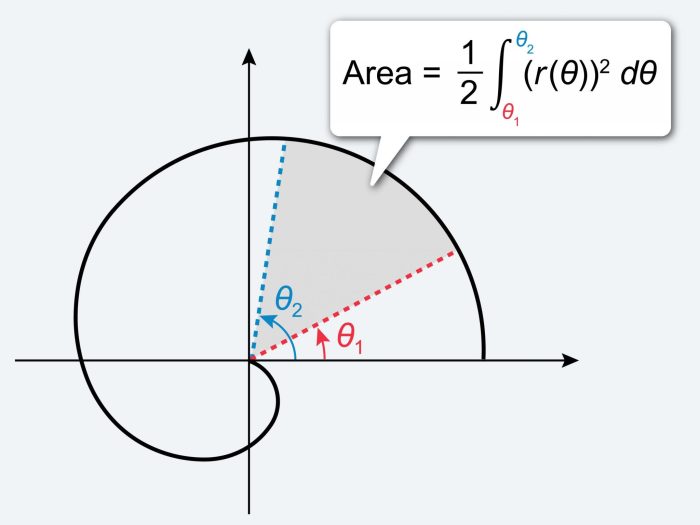
Parametric equations are useful for representing curves that are difficult to describe using rectangular equations.Polar coordinates are another way to represent points in the plane. They use two coordinates, \(r\) and \(\theta\), where \(r\) is the distance from the origin to the point and \(\theta\) is the angle between the positive \(x\)-axis and the line connecting the origin to the point.

Polar coordinates are useful for representing curves that have radial symmetry.

Converting Between Rectangular and Polar Coordinates, Ap calc bc unit 9 review

To convert from rectangular coordinates \((x, y)\) to polar coordinates \((r, \theta)\), use the following formulas:“`r = sqrt(x^2 + y^2)theta = arctan(y/x)“`To convert from polar coordinates \((r, \theta)\) to rectangular coordinates \((x, y)\), use the following formulas:“`x = r cos(theta)y = r sin(theta)“`

Examples of Using Parametric Equations to Represent Curves

* A circle of radius \(a\) can be represented by the parametric equations \(x = a \cos(t)\) and \(y = a \sin(t)\), where \(t\) is the parameter.

• A parabola can be represented by the parametric equations \(x = t\) and \(y = t^2\), where \(t\) is the parameter.
• An ellipse can be represented by the parametric equations \(x = a \cos(t)\) and \(y = b \sin(t)\), where \(a\) and \(b\) are the lengths of the semi-major and semi-minor axes, respectively, and \(t\) is the parameter.

Sequences and Series

Sequences and series are fundamental concepts in calculus that extend the notion of limits to infinite collections of numbers. They have wide applications in various fields, including physics, engineering, and finance.

Convergence and Divergence of Sequences

A sequence is an ordered list of numbers, denoted as a _n. A sequence converges to a limit L if, for any positive number ε, there exists a positive integer N such that |a _n– L| < ε for all n > N. If a sequence does not converge, it is said to diverge.

Series and Convergence Tests

A series is an infinite sum of terms, denoted as ∑ ^∞_n=1a _n. A series converges if the sequence of partial sums S _n= ∑ ⁿ_k=1a _kconverges to a finite limit. There are several convergence tests, including the Ratio Test, the Root Test, and the Comparison Test.

Series Representations of Functions

Series can be used to represent functions. For example, the exponential function e ^xcan be expressed as the series ∑ ^∞_n=0x ⁿ/n!. This representation is useful for approximating the value of e ^xfor large values of x.

Vectors and Matrices

Vectors and matrices are mathematical tools used to represent and manipulate quantities that have both magnitude and direction. They find applications in various fields, including physics, engineering, and computer graphics.Vectors are one-dimensional arrays of numbers that represent a quantity with both magnitude and direction.

They can be added, subtracted, and multiplied by scalars (numbers). Matrices are two-dimensional arrays of numbers that represent linear transformations. They can be used to solve systems of equations, find eigenvalues and eigenvectors, and perform other mathematical operations.

Vector Operations

Vectors can be added and subtracted by adding or subtracting their corresponding components. They can also be multiplied by scalars to scale their magnitude. The dot product of two vectors is a scalar that measures their similarity, while the cross product of two vectors is a vector that is perpendicular to both of them.

Matrix Operations

Matrices can be added and subtracted by adding or subtracting their corresponding elements. They can also be multiplied by scalars to scale their elements. The product of two matrices is a matrix whose elements are the sums of the products of the corresponding elements of the two matrices.

Applications of Vectors and Matrices

Vectors and matrices are used in a wide variety of applications, including:* Solving systems of equations

• Finding eigenvalues and eigenvectors
• Performing linear transformations
• Representing physical quantities such as force, velocity, and acceleration
• Creating computer graphics

FAQ Summary

What is the significance of AP Calc BC Unit 9?

AP Calc BC Unit 9 plays a crucial role in developing students’ understanding of calculus and its applications. It provides a solid foundation for further studies in mathematics, science, and engineering.

How can I prepare effectively for the AP Calc BC Unit 9 exam?

To prepare effectively, focus on understanding the concepts thoroughly, practice solving problems regularly, and seek clarification when needed. Utilize practice tests and review materials to assess your progress and identify areas for improvement.

What are the key takeaways from AP Calc BC Unit 9?

The key takeaways include the ability to apply integral calculus to solve real-world problems, solve differential equations to model various phenomena, utilize parametric equations and polar coordinates to represent curves, and analyze the convergence and divergence of sequences and series.